Задание 1. Необходимо распилить 20 бревен длинно по 5 м. каждое на бруски по 2м. и 3м.; при этом должно получиться равное количество брусков каждого размера.

Составить такой план распила, при котором будет получено максимальное число комплектов и все бревна будут распилены (в один комплект входит по одному бруску каждого размера).

Задание 2. Задачу решить симплексным методом. Сравнить полученное решение с решением, найденным геометрически.

F = 4x₁ - 2x₂ ®  max    при ограничениях:

Задание 3. Решить транспортную задачу, составив первоначальное распределение поставок методом «северо-западного» угла; предварительно составив экономико-математическую модель задачи. Найти оптимальное распределение поставок и минимальные затраты на перевозку.

Задание 4. Для следующей платежной матрицы найти нижнюю и верхнюю цену игры, минимаксную стратегию и оптимальное решение, если существует седловая точка:

.

Задание 5. Найти глобальный экстремум (наибольшее и наименьшее значения) функции z в области решений системы неравенств. Дать геометрическое решение.

Задание 6. Решить задачу выпуклого программирования методом кусочно-линейной аппроксимации:    

Указание: Отрезок изменения каждой переменной разбить на 4 части.

Задание 7. Методом динамического программирования найти оптимальное распределение средств между четырьмя предприятиями при условии, что прибыль f(x), полученная от каждого предприятия, является функцией от вложенных в него средств x. Вложения кратны ∆х, а функции f(x) заданы таблично:

s₀ = 6, ∆x = 1.

Задание 8. По данным таблицы:

а) найти r_B – выборочный коэффициент корреляции;

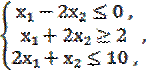
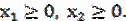
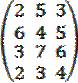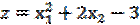
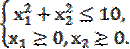
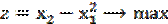
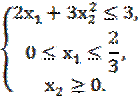
б) выборочные уравнения прямых линий регресси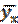и   и  .