| Общая информация » Каталог студенческих работ » МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ, ТЕОРИЯ ИГР » ДВИМБ, методы оптимальных решений |
| 16.11.2013, 12:02 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задание 1. Рацион для питания животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 100 ден. ед. и содержит: 2 ед. жиров, 4 ед. белков, 3 ед. углеводов, 4 ед. нитратов. Один килограмм корма II стоит 40 ден. ед. и содержит 8 ед. жиров, 2 ед. белков, 10 ед. углеводов, 9 ед. нитратов. Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 10 ед., белков не менее 9 ед., углеводов не менее 8 ед., нитратов не более 20 ед. Задание 2. Задачу решить симплексным методом. Сравнить полученное решение с решением, найденным геометрически. F = 2x1 - x2 ® min при ограничениях:
Задание 3. Решить транспортную задачу, составив первоначальное распределение поставок методом «северо-западного» угла; предварительно составив экономико-математическую модель задачи. Найти оптимальное распределение поставок и минимальные затраты на перевозку.
Задание 4. Магазин может завезти в различных пропорциях товары трех типов (А1, А2, А3); их реализация и прибыль магазина зависят от вида товара и состояния спроса. Предполагается, что спрос может иметь три состояния (В1, В2, В3) и не прогнозируется. Определить оптимальные пропорции в закупке товаров из условия максимизации средней гарантированной прибыли при следующей матрице прибыли:
Задание 5. Найти условный экстремум с помощью метода Лагранжа:
Задание 6. Исследовать на выпуклость следующую функцию: Задание 7. Методом динамического программирования найти оптимальное распределение средств между тремя предприятиями при условии, что прибыль f(x), полученная от каждого предприятия, является функцией от вложенных в него средств x. Вложения кратны ∆х, а функции f(x) заданы таблично:
s0 = 8, ∆x = 1. Задание 8. По данным таблицы:
а) найти rB – выборочный коэффициент корреляции; б) выборочные уравнения прямых линий регрессии | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

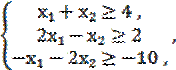
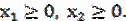
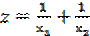 при
при 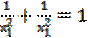 .
.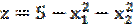 .
.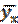 и
и 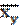 .
.