| Общая информация » Каталог студенческих работ » ЭКОНОМЕТРИКА » ТюмГУ, эконометрика |
| 09.03.2010, 10:58 | ||||||||||||||||||||||||||||||||||
Задача 1. Имеется информация за 10 лет относительно среднего дохода X и среднего потребления Y (млн. руб.):
1. Оцените коэффициенты линейной регрессии Y = b0 + b1X + e по методу наименьших квадратов. 2. Проверьте статистическую значимость оценок b0, b1, теоретических коэффициентов b0, b1 при уровне значимости a = 0,05. 3. Рассчитайте 95%-ные доверительные интервалы для теоретических коэффициентов регрессии. 4. Спрогнозируйте потребление при доходе X = 19,0 и рассчитайте 95% доверительный интервал для условного математического ожидания M(Y|X = 19,0). 5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных объемов потребления при доходе X = 19,0. 6. Оцените, на сколько изменится потребление, если доход вырастет на 3 млн. руб. 7. Рассчитайте коэффициент детерминации R2. 8. Рассчитайте F-статистику для коэффициента детерминации и оцените его статистическую значимость. Задача 2. По 15 наблюдениям получены следующие результаты:
1. Оцените коэффициенты линейной регрессии 2. Определите стандартные ошибки коэффициентов. 3. Вычислите 4. Оцените статистическую значимость коэффициентов регрессии и детерминации при уровне значимости Задача 3. Пусть определена регрессия Задача 4. Докажите, что график уравнения парной линейной регрессии всегда проходит через точку с координатами , | ||||||||||||||||||||||||||||||||||

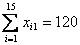 ,
, 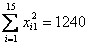 ,
, 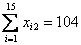 ,
,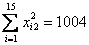
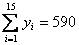
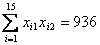 ,
,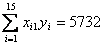
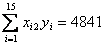
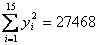
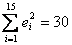
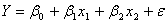 .
.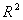
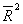 .
.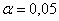 .
.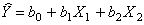 , причем
, причем 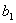
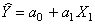
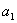
 , где
, где