| Общая информация » Каталог студенческих работ » ЭКОНОМЕТРИКА » РГТЭУ, эконометрика |
| 19.10.2013, 17:07 | ||||
Вариант 16 1. Модель спроса-предложения представляет собой: а) систему одновременных уравнений; б) регрессионную модель с одним уравнением; в) модель временного ряда; г) тренд-сезонную модель.
2. При исследовании зависимости балансовой прибыли предприятия торговли (Y, тыс. руб.) от фонда оплаты труда (Х1, тыс. руб.) и объема продаж по безналичному расчету (Х2, тыс. руб.) получена следующая модель: Y = 5933,100 + 0,916X1 + 0,065X2 + ε. Как интерпретируется коэффициент при факторном признаке X1: а) при увеличении только фонда оплаты труда на 1% балансовая прибыль предприятия торговли в среднем будет увеличиваться на 9,16%; б) при уменьшении только фонда оплаты труда на 1 тыс. руб. балансовая прибыль предприятия торговли в среднем будет уменьшаться на 916 руб.; в) при увеличении только фонда оплаты труда на 1 тыс. руб. балансовая прибыль предприятия торговли в среднем будет увеличиваться на 0,916 тыс. руб.; г) при увеличении фонда оплаты труда на 1 тыс. руб. балансовая прибыль предприятия торговли в среднем будет увеличиваться на 9,16 тыс. руб..
3. При проверке модели на автокорреляцию остатков получено следующее уравнение:
(2,35) (0,10) (0,93) (0,85) В скобках указаны значения t-статистики для коэффициентов регрессии. Табличное значение при уровне значимости α=0,05 составляет 2,07. Какой вывод можно сделать по результатам теста: а) гипотеза об отсутствии автокорреляции не отвергается (принимается); б) принимается альтернативная гипотеза о наличии в ряду остатков автокорреляции первого порядка; в) принимается альтернативная гипотеза о наличии в ряду остатков автокорреляции четвертого порядка; г) принимается альтернативная гипотеза о наличии в ряду остатков автокорреляции первого и второго порядка.
4. Исследуется потребление продукта А среди городских и сельских жителей. Сколько потребуется ввести фиктивных переменных для построения модели: а) 1; б) 2; в) 3; г) 4.
5. Какое из приведенных ниже уравнений регрессии позволяет учесть изменение не только свободного члена, но и коэффициента наклона. а) б) в) г)
6. Зависимость ежедневного среднедушевого потребления кофе (в чашках) от среднегодовой цены кофе выражается уравнением: Y = 2,34 X-0,25 ε. При увеличении цены кофе на 1% ежедневное среднедушевое потребление кофе: а) уменьшится на 0,25%; б) увеличится на 0,25%; в) уменьшится 25%; г) увеличится на 2,34%.
7. Для устранения нестационарности исследуемого временного ряда был рассмотрен ряд первых разностей, который идентифицируется моделью АР(2). Какой моделью идентифицируется исходный временной ряд: а) АРСС(2;0); б) АРПСС(2;1;0); в) АРПСС(0;1;2); г) АРСС(0;2).
8. Изучается зависимость объема ВВП (Y, млрд. долл.) от уровня прибыли в экономике (Хt, млрд. долл.). Получена следующая модель с распределенным лагом: Yt = 0,65∙Xt + 0,30∙Xt-1 + 0,10∙Xt-2 + 0,05∙Xt-3 + εt. Чему равен долгосрочный мультипликатор: а) 0,65; б) 0,95; в) 0,65; г) 1,10.
9. В соответствии с необходимым условием идентифицируемости уравнение идентифицируемо, если D + 1 = H, где: а) H – число эндогенных переменных в системе, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение; б) H – число эндогенных переменных в уравнении, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение; в) H – число экзогенных переменных в уравнении, D – число эндогенных переменных, которые содержатся в системе, но не входят в данное уравнение; г) H – число экзогенных переменных в уравнении, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение.
10. Двухшаговый метод наименьших квадратов можно применять для системы, состоящей из: а) трех сверхидентифицируемых уравнений; б) идентифицируемого, сверхидентифицируемого и неидентифицируемого уравнений; в) трех идентифицируемых уравнений; г) идентифицируемого и двух сверхидентифицируемых уравнений. Вариант 17 1. Мультиколлинеарность – это: а) зависимость последующих уровней ряда динамики от предыдущих; б) функциональная или тесная корреляционная зависимость между факторами, включенными в модель множественной регрессии; в) постоянство дисперсий остатков модели множественной регрессии.
2. При исследовании зависимости оборота розничной торговли (Y, млрд. руб.) от трех факторов: Х1 - денежные доходы населения, млрд. руб.; Х2 – численность безработных, млн. чел.; Х3 – официальный курс рубля по отношению к доллару США получена следующая модель: Y = 55,74 + 0,33X1 – 4,98X2 + 2,38X3 + ε. При увеличении только денежных доходов населения на 1 млрд. руб. оборот розничной торговли в среднем: а) увеличится на 0,33%; б) увеличится на 0,33 млрд. руб.; в) увеличится на 33%; г) останется неизменным.
3. Для проверки гипотезы об отсутствии гетероскедастичности в модели множественной регрессии были построены регрессионные модели по первым n/3 наблюдениям и последним n/3 наблюдениям. Затем получены значения суммы квадратов остатков этих моделей, рассчитано значение F-критерия Фишера, сопоставлено с табличным значением и сделан соответствующий вывод. Какой тест применялся для проверки модели на гетероскедастичность: а) тест Глейзера; б) тест Голдфельда-Квандта; в) тест Уайта; г) тест Дарбина-Уотсона.
4. Фиктивные переменные используются для: а) для ранжирования факторов по силе воздействия на результат; б) включения в регрессионную модель качественных факторов; в) для моделирования ситуации, когда значение результативного признака в текущий момент времени формируется под воздействием ряда факторов, действовавших в прошлые моменты времени.
5. Известно, что эффективность производства, описываемого функцией Y = AKαLβ ε, не зависит от масштабов. Тогда с ростом параметра α, параметр β: а) растет; б) уменьшается; в) остается неизменным; г) невозможно определить.
6. Модель авторегрессии АР(1) описывается уравнением: а) yt = b0+ b1yt-1 + εt; б) yt = b0+ b1yt-1 + b2yt-2 + εt; в) yt = b0+ b1yt-1 + εt – γ1εt-1; г) yt = εt – γ1εt-1 – γ2εt-2.
7. Метод Алмон применяется для оценки параметров модели: а) авторегрессии порядка p; б) скользящего среднего порядка q; в) с распределенным лагом с конечной величиной лага; г) с распределенным лагом с бесконечной величиной лага.
8. По данным о динамике оборота розничной торговли (Y, млрд. руб.) и дохода населения (X, млрд. руб.) была получена следующая модель с распределенными лагами: Yt = 0,46∙Xt + 0,24∙Xt-1 + 0,17∙Xt-2 + 0,14∙Xt-3 + εt. Чему равен долгосрочный мультипликатор: а) 0,46; б) 0,24; в) 0,70; г) 1,01.
9. Структурная форма модели имеет вид:
Перечислите предопределенные переменные: а) Сt, St, Rt; б) Сt, St, Rt, Rt-1; в) Rt-1, Pt, t; г) Pt.
10. Методом наименьших квадратов оценивают коэффициенты: а) приведенной формы системы одновременных линейных уравнений; б) структурной формы системы одновременных линейных уравнений; в) стандартизованной формы системы одновременных линейных уравнений.
Вариант 18 1. Укажите неправильную запись модели множественной регрессии: а) б) в) г) 2. При исследовании зависимости оборота розничной торговли (Y, млрд. руб.) от трех факторов: Х1 - денежные доходы населения, млрд. руб.; Х2 – численность безработных, млн. чел.; Х3 – официальный курс рубля по отношению к доллару США получена следующая модель: Y = 55,74 + 0,33X1 – 4,98X2 + 2,38X3 + ε. (3,08) (9,74) (-2,44) (8,37) В скобках указаны расчетные значения t-критерия Стьюдента для коэффициентов уравнения. При уровне значимости α=0,05 табличное значение tтабл= 2,07. Значение коэффициента детерминации составляет R2 = 0,746. Какое из следующих утверждений является верным: а) расчетное значение t-критерия Стьюдента для коэффициента b2 указывает на тот факт, что данный коэффициент является незначимым; б) значение коэффициента детерминации указывает на тот факт, что коэффициент b2 является незначимым; в) расчетное значение t-критерия Стьюдента для коэффициента b2 указывает на тот факт, что данный коэффициент является значимым; г) значение коэффициента детерминации указывает на тот факт, что ни один коэффициент модели не значим.
3. Модель зависимости оборота розничной торговли (Y, млрд. руб.) от трех факторов: Х1 - денежные доходы населения, млрд. руб.; Х2 – численность безработных, млн. чел.; Х3 – официальный курс рубля по отношению к доллару США в стандартизованной форме имеет следующий вид: ty = 0,33 tx1 – 4,98 tx2 + 2,38 tx3 + ε. Ранжируйте факторы в порядке возрастания их воздействия на результат: а) X1, X2, X3; б) X1, X3, X2; в) X2, X1, X3; г) X3, X1, X2.
4. При проверке модели множественной регрессии y=f(x1,x2,x3) + ε на наличие автокорреляции с помощью теста Дарбина-Уотсона было получено следующее значение d=2,18. При уровне значимости α=0,05 и числе наблюдений n=24 табличные значения составляют dн=1,10 и dв=1,66 . Какой вывод можно сделать по результатам теста: а) гипотеза об отсутствии автокорреляции не отвергается (принимается); б) вопрос об отвержении или принятии гипотезы остается открытым, так как расчетное значение попадает в зону неопределенности; в) принимается альтернативная гипотеза о наличии положительной автокорреляции; г) принимается альтернативная гипотеза о наличии отрицательной автокорреляции;
5. Для проверки гипотезы об однородности исходных данных используется: а) тест Голдфельда-Квандта; б) тест Чоу; в) тест Уайта; г) тест Дарбина-Уотсона.
6. Зависимость спроса на масло (Y, количество масла на душу населения, кг) от цены (Х1, руб.) и от величины дохода на душу населения (Х2, тыс. руб.) выражается уравнением: Y = 0,056 X1-0,858X21,126 ε. В данной модели параметр (-0,858) представляет собой: а) коэффициент эластичности спроса на масло по доходам на душу населения; б) коэффициент эластичности спроса на масло по цене; в) среднее абсолютное изменение спроса на масло при изменении его цены на 1 руб.; г) коэффициент линейной корреляции между ценой масла и количеством масла на душу населения.
7. Для устранения нестационарности исследуемого временного ряда был рассмотрен ряд первых разностей, который идентифицируется моделью CC(1). Какой моделью идентифицируется исходный временной ряд: а) АРСС(0;1); б) АРПСС(0;1;1); в) АРПСС(1;1;1); г) АРСС(1;0).
8. Временные ряды факторных переменных, сдвинутых на один или более периодов времени, называются: а) лаговыми переменными; б) фиктивными переменными; в) бинарными переменными; г) стандартизованными переменными.
9. По данным о динамике оборота розничной торговли (Y, млрд. руб.) и дохода населения (X, млрд. руб.) была получена следующая модель с распределенными лагами: Yt = 0,46∙Xt + 0,24∙Xt-1 + 0,17∙Xt-2 + 0,14∙Xt-3 + εt. Параметр модели 0,46 является: а) средним лагом; б) медианным лагом; в) краткосрочным мультипликатором; г) долгосрочным мультипликатором.
10. Структурная форма модели имеет вид:
Перечислите предопределенные переменные: а) St, Сt, Dt; б) St, Сt, Dt, Unt-1; в) Unt-1, Mt, It; Unt; г) Mt, It.
Вариант 19
1. Для определения оценок параметров линейной модели множественной регрессии путем минимизации суммы квадратов отклонений фактических значений от расчетных применяется: а) метод наименьших квадратов; б) метод максимального правдоподобия; в) метод Монте-Карло; г) метод моментов.
2. Какая запись модели множественной регрессии является неверной: а) б) в) г)
3. Получена следующая модель пространственной выборки: Y = 123,35 + 0,53X1 - 9,89X2 + ε. Как интерпретируется коэффициент при факторном признаке X2: а) при увеличении фактора X2 на 1% результативный признак в среднем будет увеличиваться на 9,89%; б) при увеличении только фактора X2 на 1% результативный признак в среднем будет уменьшаться на 9,89%; в) при увеличении только фактора X2 на 1 единицу измерения результативный признак будет в среднем уменьшаться на 9,89 своих единиц измерения; г) при увеличении только фактора X2 на 1 единицу измерения результативный признак будет уменьшаться на 9,89 своих единиц измерения.
4. Для уравнения регрессии с двумя факторными признаками значения R2 и а) при расчете R2 и б) третий фактор оказался несущественным и его включение в модель нецелесообразно; в) этот факт ничего не значит; им можно пренебречь.
5. При проверке модели множественной регрессии y=f(x1,x2,x3) + ε на наличие автокорреляции с помощью теста Дарбина-Уотсона было получено следующее значение d=1,79. При уровне значимости α=0,05 и числе наблюдений n=24 табличные значения составляют dн=1,10 и dв=1,66 . Какой вывод можно сделать по результатам теста: а) гипотеза об отсутствии автокорреляции не отвергается (принимается); б) вопрос об отвержении или принятии гипотезы остается открытым, так как расчетное значение попадает в зону неопределенности; в) принимается альтернативная гипотеза о наличии положительной автокорреляции; г) принимается альтернативная гипотеза о наличии отрицательной автокорреляции;
6. При исследовании зависимости объема потребления продукта А (y) от времени года были введены следующие фиктивные переменные: d1 (1 - если месяц зимний, 0 – в остальных случаях), d2 (1 - если месяц весенний, 0 – в остальных случаях), d3 (1 - если месяц летний, 0 – в остальных случаях) и получено следующее уравнение Y = b0 + b1d1 + b2d2 + b3d3+ ε. Чему равна разница среднемесячного объема потребления между весенними и осенними месяцами: а) b0; б) b2; в) b0 – b2; г) b0 + b2.
7. В производственной функции Кобба-Дугласа Y = AKαLβ ε параметр α соответствует коэффициенту: а) корреляции; б) детерминации; в) эластичности; г) автокорреляции.
8. Чему равен параметр авторегрессии в модели вида yt = -0,71yt-1 + εt: а) 0,71; б) 0,712; в) -0,71; г) (-0,71)2.
9. Изучается зависимость объема ВВП (Y, млрд. долл.) от уровня прибыли в экономике (Хt, млрд. долл.). Получена следующая модель с распределенным лагом: Yt = 0,65∙Xt + 0,30∙Xt-1 + 0,10∙Xt-2 + 0,05∙Xt-3 + εt. Чему равен краткосрочный мультипликатор: а) 0,05; б) 0,65; в) 0,30; г) 0,95.
10. Структурная форма модели имеет вид:
Сколько предопределенных переменных в данной системе: а) 2; б) 3; в) 4; г) 5.
Вариант 20 1. При проверке адекватности модели а) автокорреляция; б) мультиколлинеарность; в) гетероскедастичность; г) гомоскедастичность.
2. Проверка гипотезы Н0: bo = b1 = b2 = 0 позволяет: а) оценить значимость уравнения регрессии в целом; б) оценить значимость параметров модели: bo, b1, b2; в) проверить гипотезу об однородности исходных данных.
3. При исследовании зависимости балансовой прибыли предприятия торговли (Y, тыс. руб.) от фонда оплаты труда (Х1, тыс. руб.) и объема продаж по безналичному расчету (Х2, тыс. руб.) получена следующая модель: Y = 5933,100 + 0,916X1 + 0,065X2 + ε. Значение коэффициента детерминации составляет R2 = 0,814. Какая доля вариации (в %) результативного признака Y объясняется вариацией входящих в модель факторных признаков: а) 81,4; б) 0,814; в) 18,6; г) 0,816.
4. Для проверки гипотезы об отсутствии гетероскедастичности в модели множественной регрессии, построенной по 36 наблюдениям, с помощью теста Голдфельда-Квандта были построены регрессионные модели по первым m наблюдениям и последним m наблюдениям. Затем получены значения суммы квадратов остатков этих моделей, рассчитано значение F-критерия Фишера, сопоставлено с табличным значением и сделан соответствующий вывод. Чему равно значение m: а) 18; б) 12; в) 9; г) 6.
5. При исследовании зависимости объема потребления продукта А (y) от времени года были введены следующие фиктивные переменные: d1 (1 - если месяц зимний, 0 – в остальных случаях), d2 (1 - если месяц весенний, 0 – в остальных случаях), d3 (1 - если месяц летний, 0 – в остальных случаях) и получено следующее уравнение Y = b0 + b1d1 + b2d2 + b3d3+ ε. Чему равен среднемесячный объем потребления для осенних месяцев: а) b0; б) b0 + b1; в) b0 + b2; г) b0 + b3.
6. Зависимость спроса на масло (Y, количество масла на душу населения, кг) от цены (Х1, руб.) и от величины дохода на душу населения (Х2, тыс. руб.) выражается уравнением: Y = 0,056 X1-0,858X21,126 ε. При увеличении цены масла на 1% количество масла на душу населения в среднем: а) увеличится на 0,858%; б) уменьшится на 0,858%; в) уменьшится на 1,126%; г) увеличится на 1,126%.
7. Временной ряд, вероятностные свойства которого не изменяются во времени, называется: а) стационарным; б) однородным; в) нестационарным; г) интегрируемым.
8. Изучается зависимость объема ВВП (Y, млрд. долл.) от уровня прибыли в экономике (Хt, млрд. долл.). Получена следующая модель с распределенным лагом: Yt = 0,55∙Xt + 0,25∙Xt-1 + 0,14∙Xt-2 + 0,09∙Xt-3 + εt. Чему равен долгосрочный мультипликатор: а) 0,55; б) 0,25; в) 0,80; г) 1,03.
9. Модель спроса-предложения с учетом тренда записывается системой: а) независимых уравнений; б) одновременных уравнений; в) рекурсивных уравнений.
10. Система одновременных регрессионных уравнений содержит 3 эндогенные и 4 экзогенные переменные. Первое уравнение системы включает 2 эндогенные и 3 экзогенные переменные. Тогда можно утверждать, что: а) первое уравнение идентифицируемо по необходимому условию; б) первое уравнение идентифицируемо по достаточному условию; в) первое уравнение сверхидентифицируемо по необходимому условию; г) первое уравнение неидентифицируемо по необходимому условию. | ||||

 .
.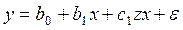 ;
; ;
;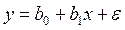 ;
;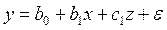 ;
;
 ;
;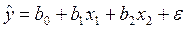 ;
;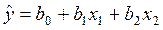 ;
; .
.
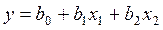
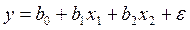 ;
; .
.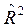 составили соответственно 0,9878 и 0,9763. При добавлении в уравнение третьего фактора получили, что R2 =0,9882 и
составили соответственно 0,9878 и 0,9763. При добавлении в уравнение третьего фактора получили, что R2 =0,9882 и  =0,9752. О чём говорит этот факт?
=0,9752. О чём говорит этот факт?
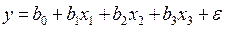 получили, что значения коэффициента детерминации и критерия Фишера позволяют говорить об адекватности модели, тогда как по критерию Стьюдента коэффициенты b1 и b2 приходится признать незначимыми. Данный факт свидетельствует о том, что в модели присутствует:
получили, что значения коэффициента детерминации и критерия Фишера позволяют говорить об адекватности модели, тогда как по критерию Стьюдента коэффициенты b1 и b2 приходится признать незначимыми. Данный факт свидетельствует о том, что в модели присутствует: