С течением времени изменяются не только уровни явлений, но и показатели их динамики – абсолютные приросты и темпы развития, поэтому для обобщающей характеристики развития, для выявления и измерения типичных основных тенденций и закономерностей и решения других задач анализа используются средние показатели временного ряда – средние уровни, средние абсолютные приросты и средние темпы динамики.

К расчету средних уровней ряда динамики часто приходится прибегать уже при построении временного ряда – для обеспечения сопоставимости числителя и знаменателя при расчете средних и относительных величин. Пусть, например, нужно построить ряд динамики производства электроэнергии на душу населения в Российской Федерации. Для этого за каждый год необходимо количество произведенной электроэнергии в данном году (интервальный показатель) разделить на численность населения в том же году (момент-ный показатель, величина которого непрерывно меняется на протяжении года). Ясно, что численность населения на тот или иной момент времени в общем случае несопоставима с объемом производства за весь год в целом. Для обеспечения сопоставимости нужно и численность населения как-то приурочить ко всему году, а это можно сделать, лишь рассчитав среднюю численность населения за год.

Часто приходится прибегать к средним показателям динамики и потому, что уровни многих явлений сильно колеблются от периода к периоду, например от года к году, то повышаясь, то понижаясь. Особенно это относится ко многим показателям сельского хозяйства, где год на год не приходится, поэтому при анализе развития сельского хозяйства чаще оперируют не годовыми показателями, а более типичными и устойчивыми среднегодовыми показателями за несколько лет.

При вычислении средних показателей динамики необходимо иметь в виду, что к этим средним показателям полностью относятся общие положения теории средних величин. Это означает прежде всего, что динамическая средняя будет типичной, если она характеризует период с однородными, более или менее стабильными условиями развития явления. Выделение таких периодов – этапов развития – в определенном отношении аналогично группировке. Если же динамическая средняя величина исчислена за период, в течение которого условия развития явления существенно менялись, т. е. период, охватывающий разные этапы развития явления, то такой средней величиной нужно пользоваться с большой осторожностью, дополняя ее средними величинами за отдельные этапы.

Средние показатели динамики должны также удовлетворять логико-математическому требованию, согласно которому при замене средней величиной тех фактических величин, из которых получена средняя, не должна изменяться величина определяющего показателя, т. е. некоторого обобщающего показателя, связанного с осредняемым показателем. Метод расчета среднего уровня ряда динамики зависит прежде всего от характера показателя, лежащего в основе ряда, т. е. от вида временного ряда.

Наиболее просто вычисляется средний уровень интервального ряда динамики абсолютных величин с равностоящими уровнями. Расчет производится по формуле простой средней арифметической:

где n – число фактических уровней за последовательные равные отрезки времени.

Сложнее обстоит дело с вычислением среднего уровня моментного ряда динамики абсолютных величин. Момент-ный показатель может изменяться почти непрерывно, поэтому чем более подробны и исчерпывающи данные о его изменении, тем более точно можно вычислить средний уровень. Более того, сам метод расчета зависит от того, насколько подробны имеющиеся данные. Здесь возможны различные случаи.

При наличии исчерпывающих данных об изменении мо-ментного показателя его средний уровень вычисляется по формуле средней арифметической взвешенной для интервального ряда с разностоящими уровнями:

где t – число периодов времени, в течение которых уровень не изменялся.

Если промежутки времени между соседними датами равны друг другу, т. е. когда мы имеем дело с равными (или примерно равными) интервалами между датами (например, когда известны уровни на начало каждого месяца или квартала, года), тогда для моментного ряда с равностоящими уровнями расчет среднего уровня ряда производим по формуле средней хронологической:

Для моментного ряда с разностоящими уровнями расчет среднего уровня ряда производится по формуле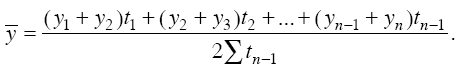

Выше шла речь о среднем уровне рядов динамики абсолютных величин. Для рядов динамики средних и относительных величин средний уровень нужно вычислять исходя из содержания и смысла этих средних и относительных показателей.

Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежемесячно, ежегодно и т. д.). Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем. Он вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени:

• расчет среднего абсолютного цепного прироста:

• расчет среднего абсолютного базисного прироста: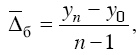

где – цепные абсолютные приросты за последовательные промежутки времени; n – число цепных приростов; У0 – уровень базисного периода.

В качестве основы и критерия правильности исчисления среднего темпа роста (как и среднего абсолютного прироста) можно использовать в роли определяющего показателя произведение цепныгх темпов роста, которое равно темпу роста за весь рассматриваемый период. Таким образом, перемножив n цепных темпов роста, мы получим темп роста за весь период:

Поставим задачу найти такой средний темп роста (р), чтобы при замене им фактических цепных темпов в формуле 8.11 остался без изменения темп роста за весь период (у1 / у1 -1). Следовательно, должно соблюдаться равенство

из которого следует:

где n – число уровней ряда динамики; Т1, Т2, Тп – цепные темпы роста.

Формула (8.1) носит название простой средней геометрической, (8.2) – средней геометрической в неявном виде.

Средний темп роста, выраженный в форме коэффициента, показыгвает, во сколько раз увеличивается уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежегодно, ежемесячно и т. п.).

Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, которая имеет место между обычными темпами роста и прироста:

Средний темп прироста (или снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или снижался) уровень по сравнению с предыдущим периодом в среднем за единицу времени (в среднем ежегодно, ежемесячно и т. п.). Средний темп прироста характеризует среднюю интенсивность роста, т. е. среднюю относительную скорость изменения уровня.

Из двух видов формулы среднего темпа роста чаще используется формула (8.2), так как она не требует вычисления всех цепных темпов роста. По формуле (8.1) расчет целесообразно производить лишь в тех случаях, когда неизвестны ни уровни ряда динамики, ни темп роста за весь период, а известны только цепные темпы роста (или прироста).